Most important MCQ questions on kinematics with solution for different competitive exams like JELET 2023, NEET, IIT-JEE, LEET exams. The questions are from two dimensional motion (2D-motion), vector, vertical motion and projectile motion.
Table of contents
- Questions on 2D motion
- Questions on vector
- Questions on circular motion
- Questions on vertical motion
- Questions on Projectile motion
Questions on two dimensional motion with answers
MCQ questions on Kinematics (2D motion) with solution for competitive exams like WBJELET 2023, LEET and other national level examinations.
1. A particle starts from rest and has an acceleration of 2 m/s2 for 10 sec. After that, it travels for 30 sec with constant speed and comes back to rest. The total distance covered by the particle is
(a) 650 m, (b) 750 m, (c) 700 m, (d) 800 m
option c
Initial velocity , u = 0
acceleration, a= 2 m/s2
time t = 10 s
Distance covered in 10 s is
s=ut+\frac{1}{2}at^{2}
s=\frac{1}{2}\times 2 (10)^{2}
s=100 m
After 10 s, the velocity of the particle is
v=u+at
v=0+ (2\times 10) = 20 m/s
Now for the next 30 s, it travels at the constant speed of 20 m/s
Distance travelled = vt = 20 \times 30 = 600 m
Total distance covered = 100 m+ 600 m = 700 m
2. A body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph
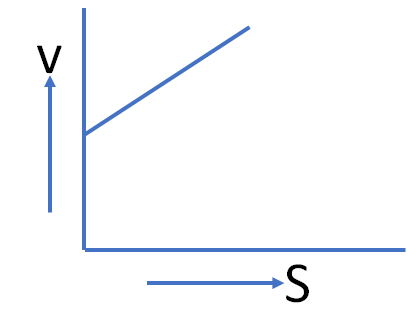
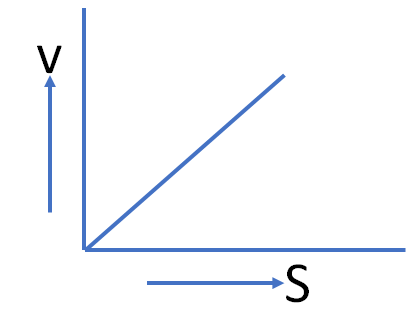
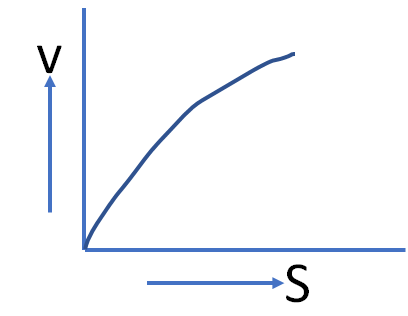
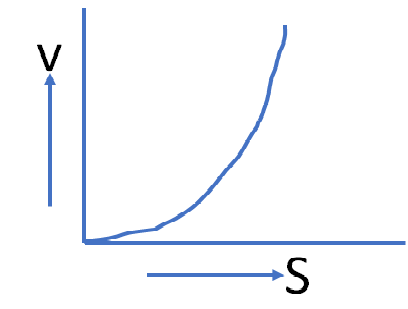
option d
The equation of a particle having final velocity v after moving a distance s is given by
v^{2}=u^{2}+2as
Where u is the initial velocity.
Here the object starts from rest. so, initial velocity u = 0
v^{2}=2as
This is the equation of a parabola. The graph will be symmetrical to v axis.
So, option (d) is the correct answer
3. The displacement of a body is given to be proportional to the cube of time elapsed. The magnitude of the acceleration of the body is proportional to
(a) \sqrt{t} , (b) t , (c) t2 , (d) t3/2
option b
Displacement is proportional to time.
s\propto t^{3}
s=k t^{3}
Where k is constant.
velocity, v=\frac{ds}{dt} = 3kt^{2}
accleration, a=\frac{dv}{dt} = \frac{d}{dt}(3kt^{2}) = 6kt
Therefore, a\propto t
4. The velocity-displacement graph of a particle moving along a straight line is shown in the figure
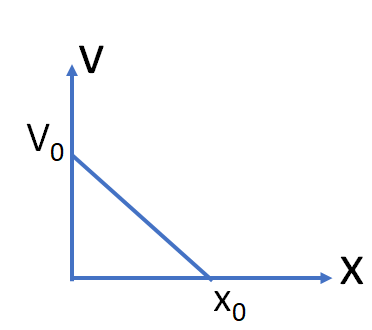
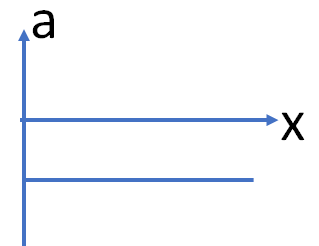
option a
The equation for the v-x graph is
v=mx+c
here m is the slope of the straight line
m=-\frac{v_{0}}{x_{0}} and c = v_{0}
so, v=-\frac{v_{0}}{x_{0}}x+v_{0}
\frac{dv}{dx}=-\frac{v_{0}}{x_{0}}
acceleration, a=v\frac{dv}{dx}
a=-\frac{v_{0}}{x_{0}}[-\frac{v_{0}}{x_{0}}x+v_{0}]
a=\frac{v_{0}^{2}}{x_{0}^{2}}x-\frac{v_{0}^{2}}{x_{0}}
if we compare this equation with y=mx+c
here m is the slope (positive), m = \frac{v_{0}^{2}}{x_{0}^{2}}
and intercept, c = -\frac{v_{0}^{2}}{x_{0}}which is negative
So, the right graph is option (a) which has positive slope and negative intercept
5. The relation between time t and distance x is t=ax^{2}+bx where a and b are constants. The acceleration is
(a) 2bv^{3}(b) -2abv^{2} (c) 2av^{2}, (d) -2av^{3}
option d
t=ax^{2}+bx
differentiating with respect to t
\frac{d}{dt}(t)=\frac{d}{dt}(ax^{2}+bx)
1=2ax\frac{dx}{dt}+b\frac{dx}{dt}
\frac{dx}{dt} = v is the velocity
1=2axv+bv
v(2ax+b) = 1
2ax+b = \frac{1}{v}
Again differentiating with respect to t
2a\frac{dx}{dt} + 0 = -\frac{1}{v^{2}}\frac{dv}{dt}
2av = -\frac{1}{v^{2}} a
where acceleration, a=\frac{dv}{dt}
a = -2av^{3}
6. A particle loaded at x=0 and t=0, starts moving along with a velocity v, that varies as v=\alpha \sqrt{x}. The displacement of the particle varies with time as
(a) t2 , (b) t , (c) t1/2 (d) t3
option a
v=\alpha \sqrt{x}
\frac{dx}{dt}=\alpha \sqrt{x}
\frac{dx}{\sqrt{x}}=\alpha dt
\int_{0}^{x}\frac{dx}{\sqrt{x}}=\int_{0}^{t}\alpha dt
2 \sqrt{x}=\alpha t
x=\frac{\alpha^{2}t^{2}}{4}
x \propto t^{2}
7. A car accelerates from rest at a constant rate \alpha for some time, after which it decelerates at a constant rate \beta and comes to rest. If the total time elapsed is t, then the maximum velocity acquired by the car is
(a) (\frac{\alpha ^{2}+\beta ^{2}}{\alpha \beta })t
(b) (\frac{\alpha ^{2}-\beta ^{2}}{\alpha \beta })t
(c) \frac{(\alpha + \beta )t}{\alpha \beta }
(d) \frac{\alpha \beta t}{\alpha +\beta }
option d
Let V be the maximum velocity.
The initial velocity of the car is 0 and let the velocity become V after a time t_{1}. Then
V = 0 + \alpha t_{1}
V = \alpha t_{1}
t_{1} = \frac{V}{\alpha }
Then it decelerates at a rate \beta and comes to rest after a time t_{2}.
So. after time t_{2}, the velocity is zero.
0 = V - \beta t_{2}
In this case the initial velocity is V.
V = \beta t_{2}
t_{2} = \frac{V}{\beta }
Total time t = t_{1}+t_{2}
t=\frac{V}{\alpha }+\frac{V}{\beta }
t = V(\frac{1}{\alpha }+\frac{1}{\beta })
V=\frac{\alpha \beta t}{\alpha +\beta }
MCQ questions with answers on vector
Three important mcq questions on kinematics (Vectors) are given with answer.
1. If \vec{P}.\vec{Q}=PQ , then the angles between \vec{P} and \vec{Q} is
(a) 450 , (b) 300 , (c) 600 , (d) 00
option d
\vec{P}.\vec{Q}=PQ
PQCos\theta = PQ
Cos\theta = PQ/PQ
Cos\theta= 1
\theta = 00
2. If vectors \vec{P}=a\hat{i}+a\hat{j}+3\hat{k} and \vec{Q}=a\hat{i}-2\hat{j}-\hat{k} are perpendicular to each other, then the positive value of a is
(a) 3, (b) 1, (c) 2, (d) 0
option a
The angle between the two vectors is 900 . So, the dot product of the vectors is 0.
\vec{P}.\vec{Q} = PQCos900 = 0
\vec{P}.\vec{Q} = 0
(a\hat{i}+a\hat{j}+3\hat{k}).(\vec{Q}=a\hat{i}-2\hat{j}-\hat{k}) = 0
a^{2}-2a-3=0
(a-3)(a+1) = 0
a=3 or -1
So, the positive value of a is 3.
3. Vectors \vec{A}, \vec{B}and \vec{C} are such that \vec{A}.\vec{B} = 0and \vec{A}. \vec{C} = 0. Then the vector parallel to \vec{A} is
(a) \vec{B} and \vec{C}, (b) \vec{A} \times \vec{B} , (c) \vec{B} + \vec{C}, (d) \vec{B} \times \vec{C}
option d
The dot product of \vec{A} and \vec{B} is 0. So, \vec{A} is perpendicular to \vec{B}. Similarly the dot product of \vec{A} and \vec{C} is 0, So, \vec{A} is perpendicular to \vec{C}. So \vec{A} is perpendicular to both \vec{B} and \vec{C}.
Again we know that the direction of the vector \vec{B} \times \vec{C} is perpendicular to both \vec{B} and \vec{C}.
So, ( \vec{B} \times \vec{C}) vector is parallel to \vec{A}
MCQ questions with answers on circular motion (Kinematics)
1. A particle revolves round a circular path. The acceleration of the particle is inversely proportional to
(a) mass of the particle, (b) radius, (c) velocity, (d) both a and b
option b
The acceleration of a particle moving in a circular path is given by
a=\frac{v^{2}}{r}
So, a is inversely proportional to r (radius).
2. A particle of mass m moves with constant speed along a circular path of radius r under the action of force F. Its speed is
(a) \sqrt{\frac{Fr}{m}}, (b) \sqrt{\frac{F}{r}}, (c) \sqrt{Fmr} , (d) \sqrt{\frac{F}{mr}}
option a
Force, F=m\frac{v^{2}}{r}
v^{2}=\frac{Fr}{m}
v=\sqrt{\frac{Fr}{m}}
3. The position of a particle moving in the x-y plane at any time t is given by x=(3t^{2}-6t)m and y=(t^{2}-2t) m. Select the correct statement
(a) acceleration is 0 at t=0
(b) velocity is 0 at t=0
(c) velocity is 0 at t=1 s
(d) velocity and acceleration of the particle is never zero
option c
x=(3t^{2}-6t)
velocity, \frac{dx}{dt}=6t-6
at t=1, velocity in X-direction is = 6\times 1-6 = 0
y=(t^{2}-2t)
\frac{dy}{dt} = 2t-2
at t=1, velocity in Y-direction is = 2\times 1-2=0
So, at t=1s velocity is zero.
MCQ questions on vertical motion (Kinematics)
MCQ questions on Kinematics (Vertical motion of particles) with answers for WBJEE JELET 2023 Physics, LEET, NEET and KVPY, CUET examinations.
1. A ball is dropped from the top of a building 100 m high. At the same instant another ball is thrown upwards with a velocity of 40 m/s from the bottom of the building. The two balls will meet after
(a) 3 s, (b) 2 s, (c) 2.5 s, (d) 5 s
option c
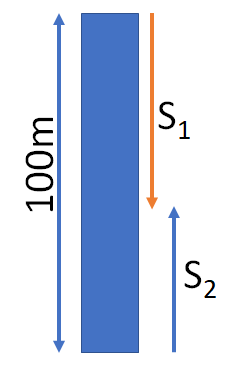
Let the two balls meet after a time t.
In time t, one ball will go a distance
S_{1}=\frac{1}{2}gt^{2}
The second ball is thrown upwards with a speed 40 m/s. So, it will go a distance
S_{2}=ut-\frac{1}{2}gt^{2}
u = 40m/s, so
S_{2}=40t-\frac{1}{2}gt^{2}
S_{1}+S_{2}=100 m
\frac{1}{2}gt^{2}+40t-\frac{1}{2}gt^{2}=100
40t=100
t = 100/40 = 2.5 s
2. A ball is released from the top of a tower of height h meters. It takes T seconds to reach the ground. What is the position of the ball at T/3 second
(a) 8h/9 meters from the ground
(b) 7h/9 meters from the ground
(c) h/9 meters from the ground
(d) 17h/18 meters from the ground
option a
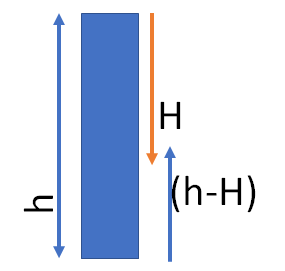
In T seconds, the ball reach the ground, so
h=\frac{1}{2}gT^{2}
In T/3, the ball will go a distance
H=\frac{1}{2}g(T/3)^{2}=\frac{1}{2}\frac{gT^{2}}{9}=\frac{h}{9}
So, the distance from the ground is h-H = h-\frac{h}{9} = \frac{8h}{9}
3. From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is
(a) 2gH=n^{2}u^{2} (b) gH=(n-2)^{2}u^{2} (c) 2gH=nu^{2}(n-2) (d) gH=(n-2)u^{2}
option c
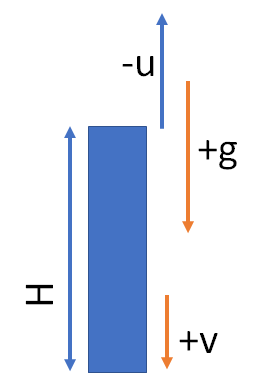
At highest point, upward velocity becomes zero.
Let t be the time to reach the highest point.
0=-u+gt
We are taking upward direction as negative and downward direction as positive. So u is negative and g is positive.
t = \frac{u}{g}
On reaching the ground, the speed becomes v.
v^{2}=(-u)^{2}+2gH
v^{2}=u^{2}+2gH
v=\sqrt{u^{2}+2gH} ——(1)
Let in time T, the ball reach ground.(In time T, the ball reach the highest point and come to ground)
again, v=-u+gT—-(2)
Equating equation (1) and (2)
\sqrt{u^{2}+2gH}=-u+gT
According to the question, T = nt =\frac{nu}{g}
\sqrt{u^{2}+2gH}=-u+g(\frac{nu}{g} )
\sqrt{u^{2}+2gH}=-u+nu
\sqrt{u^{2}+2gH}=(n-1)u
{u^{2}+2gH}=(n-1)^{2}u^{2}
2gH=(n-1)^{2}u^{2}-u^{2}
2gH=[(n-1)^{2}-1]u^{2}}
2gH=[(n^{2}-2n+1)-1]u^{2}
2gH=n(n-2)u^{2}
MCQ question and solution on projectile motion (kinematics)
Three mcq questions on Kinematics (projectile motion) for WBJEE JELET 2023, NEET 2023, JEE, LEET exams. The solution for all mcq questions are given for projectile motion.
1. An arrow is projected into air. Its time of flight is 5 s and range 200 m. What is the maximum height reached by it. (take g=10 ms-2 )
(a) 31.25 m, (b) 24.5 m, (c) 18.25 m, (d) 46.75 m
option a
Time of flight in projectile motion is
\frac{2usin\theta }{g}=5
\frac{usin\theta }{g}=\frac{5}{2}
Maximum height reached,
h=\frac{u^{2}Sin^{2}\theta }{2g}
h=\frac{g}{2}\frac{u^{2}Sin^{2}\theta }{g^{2}}
h=\frac{g}{2} \times (\frac{5}{2})^{2}
h=\frac{10}{2} \times (\frac{5}{2})^{2}=31.25 m
2. A particle is projected from the ground with an initial speed of u at an angle \theta with horizontal. The average velocity of the particle between its point of projection and highest point of trajectory is
(a) \frac{u}{2}\sqrt{1+2Cos^{2}\theta }, (b) \frac{u}{2}\sqrt{1+Cos^{2}\theta }(c) \frac{u}{2}\sqrt{1+3Cos^{2}\theta } (d) uCos\theta
option c
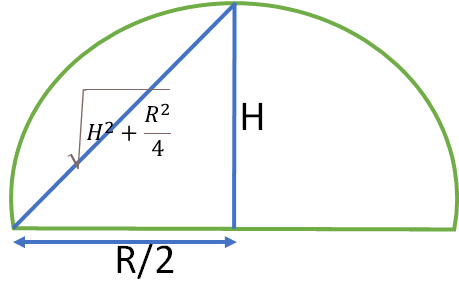
Time of flight, T=\frac{2usin\theta }{g}
Time to reach the highest point is T/2
here, H=\frac{u^{2}Sin^{2}\theta }{2g}
R=\frac{u^{2}Sin2\theta }{g}
Average velocity to reach the highest point = Displacement / Time
=\frac{\sqrt{H^{2}+\frac{R^{2}}{4}}}{T/2}
=\frac{\sqrt{(\frac{u^{2}Sin^{2}\theta }{2g})^{2}+\frac{(\frac{u^{2}Sin2\theta }{g})^{2}}{4}}}{\frac{2usin\theta }{2g}}
=\frac{u^{2}}{2g}\frac{\sqrt{Sin^{4}\theta +2Sin^{2}\theta Cos^{2}\theta }}{\frac{2usin\theta }{2g}}
=\frac{uSin\theta }{2Sin\theta }\sqrt{Sin^{2}\theta + 2Cos^{2}\theta}
=\frac{u}{2}\sqrt{1+Cos^{2}\theta + 2Cos^{2}\theta}
= \frac{u}{2}\sqrt{1+3Cos^{2}\theta }
3. A projectile is given an initial velocity of (\hat{i}+2\hat{j}) m/s, where \hat{i} is along the ground and \hat{j} is along the vertical. If g=10 ms-2 , the equation of its trajectory is
(a) y=x-5x^{2} (b) y=2x-5x^{2} (c) 4y=2x-5x^{2} (d) 4y=2x-25x^{2}
option b
We know that, \vec{u}=ucos\theta \hat{i}+usin\theta \hat{j} = \hat{i}+2\hat{j}
so, ucos\theta=1and usin\theta = 2
therefore, tan\theta = 2
The equation of a projectile is
y=xtan\theta -\frac{1}{2}\frac{gx^{2}}{u^{2}Cos^{2}\theta }
y=2x -\frac{1}{2}\frac{10x^{2}}{1^{2}}
y=2x-5x^{2}