Important MCQ on laws of motion with solution for exams like WBJELET 2023, CUET, LEET, NEET, IIT-JEE. There are ten questions on kinetic energy and momentum, friction, mass pulley system, incline plane, cyclist on a road, banking of a road etc.
1. A 4 kg mass and 1 kg mass are moving with equal kinetic energies. The ratio of the magnitudes of their linear momenta is
(a) 1:2 , (b) 1:1 , (c) 2:1 , (d) 4:1
option c
The relation between the kinetic energy and linear momenta is
Kinetic energy, E=\frac{1}{2}mv^{2}
E=\frac{1}{2m}m^{2}v^{2}
E=\frac{1}{2m}p^{2}
p=mv is the momentum
Let 4 kg mass has momenta p1 and 1 kg mass has momentum p2
E_{1}=\frac{1}{2\times 4}p_{1}^{2}
E_{1}=\frac{1}{8}p_{1}^{2}
E_{2}=\frac{1}{2\times 1}p_{2}^{2}
E_{2}=\frac{1}{2}p_{2}^{2}
Here E_{1}=E_{2}
\frac{1}{8}p_{1}^{2}=\frac{1}{2}p_{2}^{2}
\frac{p_{1}^{2}}{p_{2}^{2}}=4
\frac{p_{1}}{p_{2}}=2
p_{1}:p_{2}=2:1
MCQ Questions with answers on Friction
2. A body of mass of m is placed on a rough surface with coefficient of friction (\mu) inclined at \theta. If the mass is in equilibrium, then
(a) \theta =\tan^{-1}(\frac{m}{\mu}) (b) \theta =\tan^{-1}(\mu) (c) \theta =\tan^{-1}(\frac{\mu}{m}) (d) \theta =\tan^{-1}(\frac{1}{\mu})
option b
The weight of the body mg acts in the downward direction.
N is the normal reaction of the inclined plane.
mg can be resolved in the two directions as mgcos\theta and mgSin\theta as shown in the figure.
Here N =mgcos\theta
So, the frictional force f = \mu N = \mu mgcos\theta
As the body is in equilibrium,
f = mgSin\theta
\mu mgcos\theta =mgSin\theta
tan\theta = \mu
\theta = \tan^{-1}(\mu)
3. A cyclist moving with a speed of 4.9 m/s on a level road can take a sharp circular turn of radius 4 m, then coefficient of friction between the cycle tyres and road is
(a)0.51 (b) 0.41 (c) 0.71 (d) 0.61
option d
speed of the cyclist, v = 4.9 m/s
radius of the circular turn, r = 4 m
A centripetal force (\frac{mv^{2}}{r}) is required to move in a circular path.
Where m is the mass of the cyclist.
The frictional force (\mu mg) should supply this required centripetal force.
\frac{mv^{2}}{r} = \mu mg
\frac{v^{2}}{rg} = \mu
\mu=\frac{v^{2}}{rg}
\mu=\frac{(4.9)^{2}}{4 \times 9.8}
\mu=0.61
4. A horizontal force of 10 N is necessary to just hold a block against a wall. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
(a) 20 N, (b) 50 N, (c) 100 N, (d) 2 N
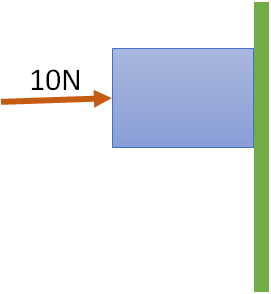
option d
The block to hold against the wall, the frictional force (Fs )must be equal to the weight (W) of the body.
So, Fs = W
The normal reaction of the wall is N = 10 N (as the force acting against the wall is 10 N)
F_{s}=\mu_{s}N
F_{s}=0.2 \times 10=2 N
So, Fs = W = 2 N
The weight of the body is 2 N
MCQ on Mass pulley system
5. Two masses M1 = 5 kg and M2 = 10 kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown in the figure. When the masses are released, then the acceleration of masses will be
(a) g (b) g/2 (c) g/3 (d) g/4
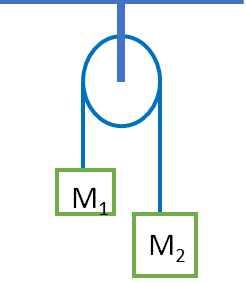
option C
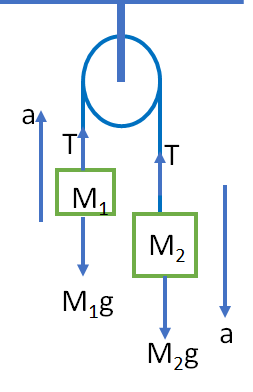
M2 is greater than M1 . So, M2 will move downwards and M1 will move upwards.
Let T be the tension in the string.
Let a be the acceleration, then net force on M2 is
M_{2}a=M_{2}g-T
T=M_{2}(g-a)
For mass M1
M_{1}a=T-M_{1}g
Put the value of T here
M_{1}a=M_{2}(g-a)-M_{1}g
(M_{1}+M_{2})a=M_{2}g-M_{1}g
(M_{1}+M_{2})a=(M_{2}-M_{1})g
a=\frac{(M_{2}-M_{1})}{(M_{1}+M_{2})}g
a=\frac{(10-5)}{(10+5)}g
a=\frac{5}{15}g
a=\frac{g}{3}
6. Three equal weights 3 kg each are hanging on a string passing over a frictionless pulley as shown in figure. The tension in the string between II and III will be (take g=10 ms-2)
(a) 5 N (b) 6 N, (c) 10 N, (d) 20 N
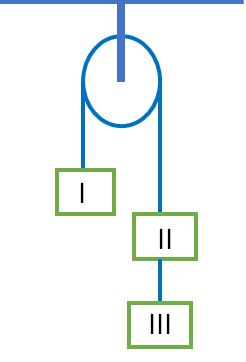
option d
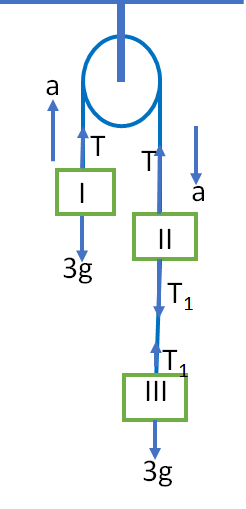
Let a be the acceleration of all the three masses.
The tension at different position is shown in figure.
Let T1 be tension between II and III.
For the body I (mass 3kg)
T-3g = 3a —–(1)
For the body II (mass 3kg)
The net force is acting downward
3g+T1 – T = 3a —-(2)
For the body III (mass 3kg)
3g-T1 = 3a —-(3)
Add all the three equations
(T-3g)+(3g+T1 – T)+(3g-T1) = 3a+3a+3a
3g=9a
a = 3/9 g = g/3
Put the value of a=g/3 in equation (3)
3g-T1 = 3a
3g-T1 = 3(g/3)
3g-T1 = g
T1 = 2g
T1= 2(10) = 20 N
7. Consider the system shown in figure. The pulley and the string are light and all the surfaces are frictionless. The tension in the string is (g=10 ms-2 )
(a) 0 N (b) 1 N (c) 2 N (d) 5 N

option d
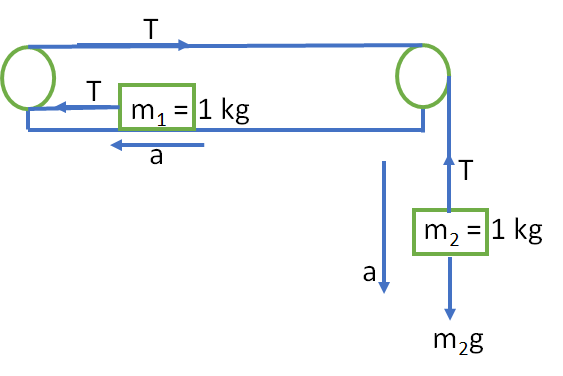
The forces acting on m1 and m2 are shown in figure.
Let a be the acceleration of the two masses.
T be the tension of the string. As all the strings are frictionless, T will be same in all the string.
For mass m1
m_{1}a=T
or 1\times a=T
T=a
and
m_{2}a=m_{2}g-T
a=g-T
put the value of a=T in this equation
T=g-T
2T=g
T=g/2=10/2=5 N
MCQ on incline plane
8. A block rests on a rough inclined plane making an angle of 300 with the horizontal. The coefficient of static friction between the blocks and the plane is 0.8. If the frictional force on the block is 10 N, the mass of the block (in kg) is (take g=10 ms-2 )
(a) 1.6 (b) 4.0 (c) 2.0 (d) 2.5
option c
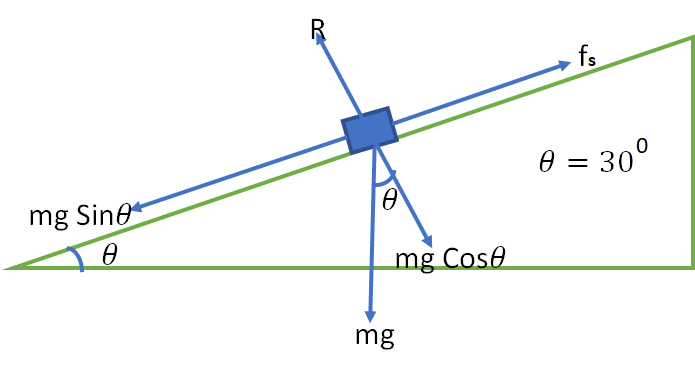
The frictional force, f_{s}=10 N
The component of mg along the direction of the slope is mgSin\theta = mgSin30^{0} = \frac{mg}{2}=\frac{m\times 10}{2}=5m
This force balances the frictional force.
Therefore,
mgSin\theta=f_{s}
5m=10
m=2 kg
9. A block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6. What should be the minimum value of force P, such that the block does not move downward? (take g=10 ms-2 )
(a) 30N, (b) 32N, (c) 40N, (d) None of the above
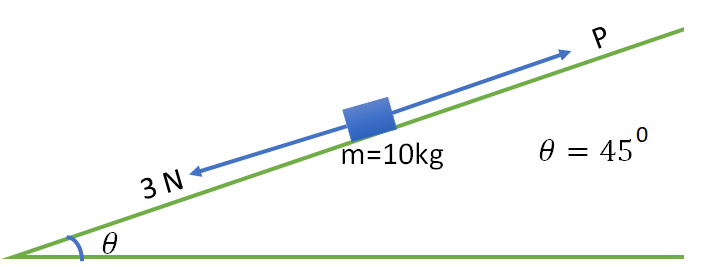
option b
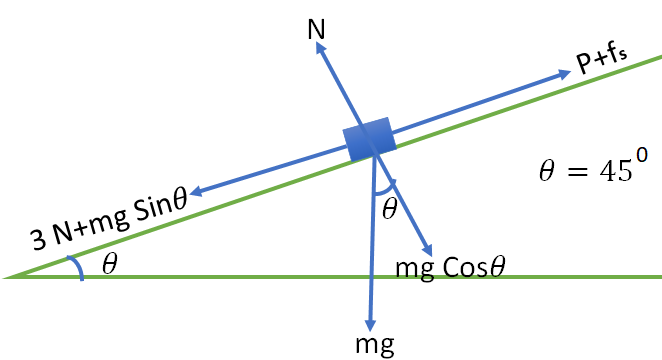
The component of mg are mgCos\theta and mgSin\theta as shown in the figure.
The normal reaction N=mgCos\theta
The frictional force, f_{s}=\mu N = \mu mgCos\theta
The block does not move downward, so the force along the inclination is zero.
Therefore,
3+mgSin\theta=P+\mu mgCos\theta
P = 3+ mg(Sin\theta-\mu Cos\theta)
\mu = 0.6 and \theta = 45^{0}
P = 3+ mg(Sin45^{0}-0.6 \times Cos45^{0})]
P = 3+ \frac{10\times 10}{\sqrt{2}}(1-0.6)
P=31.28 N
P=32 N (approximately)
10. A block is kept on a frictionless inclined surface with angle of inclination \alpha . The incline is given an acceleration a to keep the block stationary. Then a is equal to
(a) gCosec\alpha (b) gtan\alpha (c) gtan\alpha (d) g
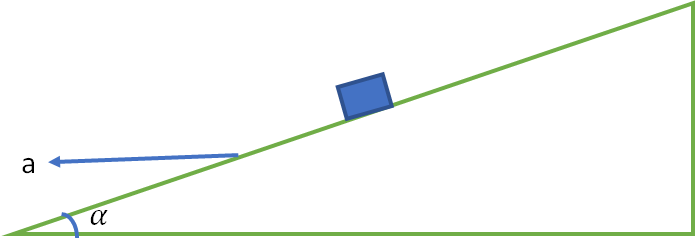
option b
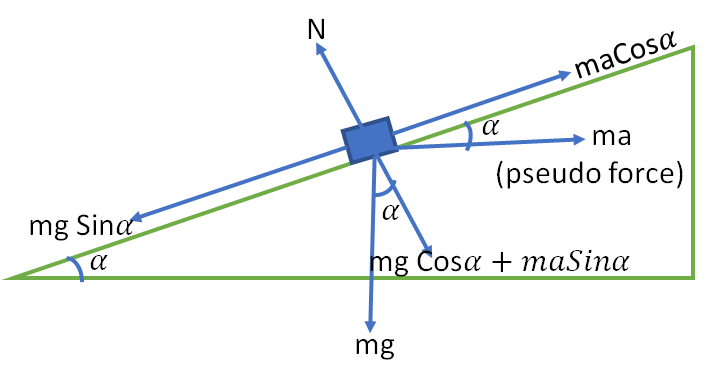
A pseudo force (ma) will act on the block in the accelerated frame of reference. The direction of this force will be opposite to the direction of acceleration.
The component of ma is the direction of inclination is maCos\alpha
The block will be in stationary if the two forces along the incline is equal. Then
maCos\alpha=mgSin\alpha
a=g\frac{Sin\alpha}{Cos\alpha}
a=gtan\alpha