post office box experiment in physics | practical

TO VERIFY LAWS OF RESISTANCES IN SERIES BY POST OFFICE BOX

Theory

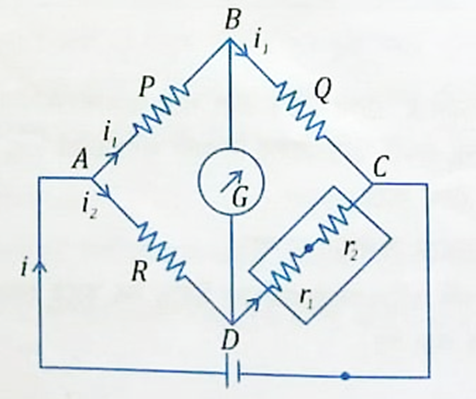
To verify laws of resistances in series, a post office box is used to measure unknown resistance. It works on the principle of Wheatstone bridge. P, Q, R and S be the four resistances of the Wheatstone bridge as shown in figure 1. Here, P, Q and R are the known resistances and S is the unknown resistance. A galvanometer is connected between B and D. When the galvanometer current is zero (null condition ), the relation between P, Q, R and S is
$\frac{P}{Q} = \frac{R}{S}$

$S= \frac{Q}{P}R$
Where, S is the equivalent resistance of two resistances connected in series. P and Q are the resistances in the ratio arm and R is the resistance of the rheostat arm.
Or, $S= r_{1}+r_{2}$

Procedure for post office box experiment or practical in physics (Need not to write in your laboratory notebook)

Two known resistances are connected in series.
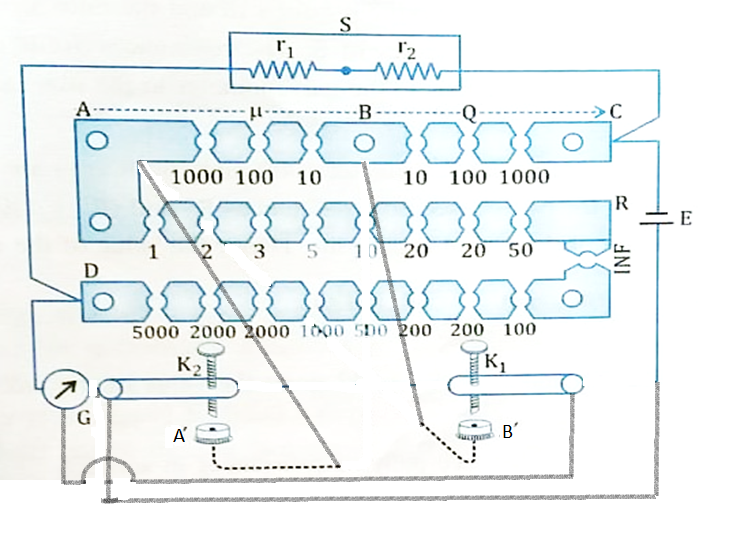
All circuit elements are connected as shown in Figure 2.
To check the correctness of the circuit, first 10 $\Omega$ resistance is put in the two ratio arms i.e. P and Q. A zero resistance is put in the third arm. Then the battery key is pressed first and after that the galvanometer key is pressed. Notice the direction of galvanometer scale deflection (say left)
Now make the resistance of the third arm infinity or maximum. Check the direction of galvanometer scale deflection after pressing the two keys. If the deflection of the galvanometer is opposite (say right) to the previous one, then the connection is correct.
Now change the resistance of the third arm, so that the deflection of the galvanometer is narrowed in both sides. Find a resistance R and R+1 in the third arm, for which the deflection of the galvanometer is slight left and slight right.
1. $\frac{P}{Q} =\frac{R}{S}$
  $\frac{10}{10} =\frac{R}{S}$
  $R=S$
  So, the unknown resistance will be in between R and R+1.
Now, set the resistances in the ratio arm as 100:10. So,
$\frac{P}{Q} =\frac{R}{S}$
$\frac{100}{10} =\frac{R}{S}$
R=10S
So, R will be 10 times of S.
Find two resistances in the third arm R₁ and (R₁+1) to make the galvanometer deflection very low and opposite.
Therefore, the unknown resistance will be in between $\frac{R_{1}}{10}$ and $\frac{R_{1}+1}{10}$ .
Now, set the ratio arm as 1000:10.
$\frac{P}{Q} =\frac{R}{S}$
$\frac{1000}{10} =\frac{R}{S}$
R=100S
So, R will be 100 times of S.
Find two resistances in the third arm R₂ and (R₂+1) to make the galvanometer deflection very low and opposite
Therefore, the unknown resistance will be in between $\frac{R_{2}}{100}$ and $\frac{R_{2}+1}{100}$ .

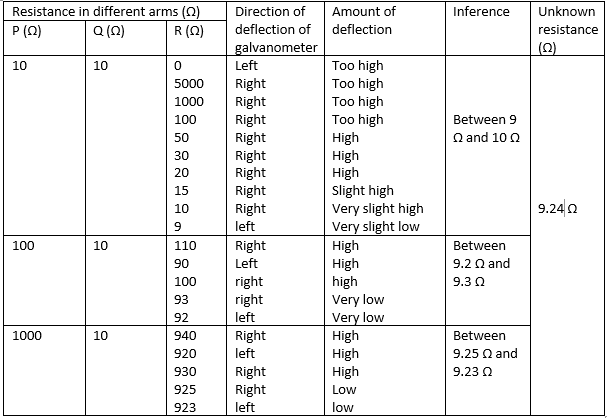
Result

Table for finding equivalent resistance in series connection

Precautions or Discussions

The battery key should be pressed first and then the galvanometer key.
All plugs should be filled tightly.
Low currents should be passed to the P.O box.

Viva questions on post office box experiment in physics | practical (TO VERIFY LAWS OF RESISTANCES IN SERIES BY POST OFFICE BOX)

1. Why is the instrument called P.O (post office ) box ?

Ans: This instrument is used to measure the unknown resistances of electric cable and telegraphic wires. It is used by the postal department to find resistance of communication wires. This is why the name of this instrument is post office (P.O) box.

2. In which principle does the post office box works?

Ans: It works on the principle of Wheatstone bridge.

3. State the principle of Wheatstone bridge.

Ans: The condition at which the galvanometer deflection is zero is called null condition. At null condition, the relation between the four resistances P, Q, R and S is
$\frac{P}{Q} =\frac{R}{S}$

4. How do you know the connection is correct.

Ans: See procedure no. (3)