The important questions on uniform circular motion with answers are discussed. These questions are important for polytechnic first year physics course, class 9, class 11 and B. Tech or B.E. first year physics course.
Table of contents
1. MCQ questions and answers on circular motion
2. Short answer type questions on uniform circular motion
3. Numerical problems on uniform circular motion
MCQ questions and answers on circular motion
1. Express rpm to radians per second.
(a) \frac{\pi}{60} rad/sec, (b) \frac{2\pi}{60} rad/sec, (c) \frac{3\pi}{60} rad/sec, (d) \frac{4\pi}{60} rad/sec
option b
Full form of rpm is revolution per minute. In circular motion the angular displacement for one complete revolution is 2\pi radian.
So, 1rpm = \frac{2\pi}{60} rad/sec
2. For an object under uniform circular motion, which of the following remains constant
(a) Kinetic energy, (b) speed, (c) magnitude of acceleration, (d) all of these
option d
In uniform circular motion, the speed (v) remains constant. So, the kinetic energy \frac{1}{2}mv^{2}, also remains constant. The magnitude of acceleration ( \frac{mv^{2}}{r}) also remains constant. But the direction of acceleration always changes. So, answer is option (d) all of these remain constant
3. What is the relation between frequency ( \nu) and time period (T) in uniform circular motion?
(a) \nu = T, (b) \nu = 1/T, (c) \nu = T2 , (d) None of these
option b
Frequency is defined as the number of cycles per unit time. Where as time period is the time for one complete cycle. If T is the time period, then in T sec 1 cycle is completed. So in 1 sec 1/T cycles will be completed and that is the frequency.
\nu = 1/T
4. The relation between angular velocity ( \omega) and linear velocity (v) is
(a) \omega = vr, (b) v= \omega/r, (c) v = \omegar, (d) None of these
option c
The relation between angular velocity and linear velocity is v = \omegar
The relation between angular acceleration ( \alpha) and linear acceleration (a) is a = \alphar ,
r is the radius of the circular path
5. The angular velocity of the minute hand of a clock is
(a) \frac{\pi}{30} rad/sec, (b) \frac{\pi}{60} rad/sec, (c) \frac{\pi}{1800} rad/sec, (d) \frac{\pi}{3600} rad/sec
option b
The minute hand completes one revolution in 60 min or 3600 sec. The angular displacement for one complete cycle is 2 \pi.
So, angular velocity of minute hand is
angular \hspace{0.2cm} velocity=\frac{angular \hspace{0.2cm} displacement}{time}
angular \hspace{0.2cm} velocity=\frac{2\pi}{3600} rad/s
angular \hspace{0.2cm} velocity=\frac{\pi}{1800}rad/s
Short answer type questions and answers
Five important short answer type questions on uniform circular motion with answers for board exams, polytechnic first year physics or other examinations.
1. What is centripetal force?
When a particle moves in a uniform circular motion, a force acts towards the centre of he circular path. This force is called centripetal force. If m is the mass of the particle moving with uniform velocity v in a circular path of radius r, then the centripetal force is
F=m\frac{v^{2}}{r}
2. How centripetal force is related to angular velocity?
The relation between angular velocity ( \omega) and linear velocity v is v = \omegar, where r is the radius of the circular path.
Centripetal force,
F=m\frac{v^{2}}{r}
Put the value of v = \omegar
F=m\frac{(\omega r)^{2}}{r}
F=m\frac{\omega^{2} r^{2}}{r}
F=m\omega^{2} r
3. Why centrifugal force is called a pseudo force?
Centrifugal force is not a real force. It exists only in non-inertial reference frame or rotating frame of reference. It can not be observed from inertial frame of reference.
4. Why banking of road is necessary?
Banking of road is necessary to supply the required centripetal force to the vehicles in a turn. The outer edge of the road is raised above the inner edge of the road in a turn of a road. The angle at which the outer edge is raised is known as angle of banking.
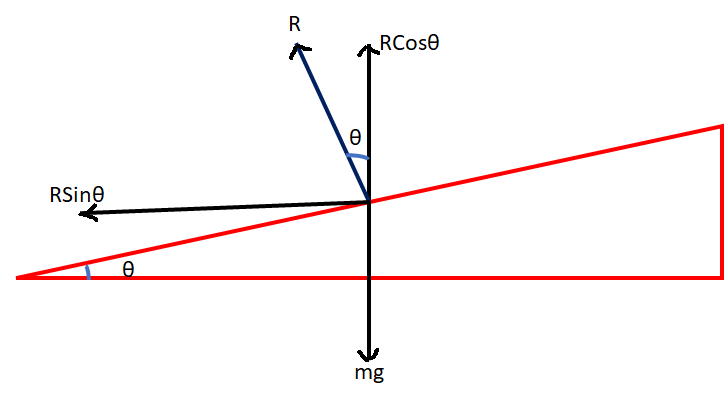
In the figure, the angle of banking is \theta.
If the radius of the circular turn is r, m is the mass of the vehicle and R is the normal reaction of the road.
The weight of the vehicle mg acts downward.
The normal reaction R is resolved in two directions.
The vertical component RCos\theta balances the weight of the body.
The horizontal component RSin\theta provides the necessary centripetal force to take a safe turn.
Then RCos\theta = mg
RSin\theta =\frac{mv^{2}}{r}
m is the mass of the vehicle and v is the velocity.
\frac{RSin\theta}{RCos\theta}=\frac{\frac{mv^{2}}{r}}{mg}
tan\theta =\frac{v^{2}}{rg}
v=\sqrt{rgtan\theta }
here v is the maximum velocity at which a vehicle can take a safe turn.
5. Cyclist is riding on a cycle with speed 𝑣 while turning on a circular path of radius 𝑟, he leans at an angle 𝜃 with the vertical. Then what will be the value of 𝑡𝑎𝑛 𝜃? Or Why a cyclist bend while turning on a curved road.
A cyclist bends on a turning road to provide the centripetal force.
Let the cyclist bends at angle \theta with the vertical while taking a turn on a road.
The ground exerts a reactional force on the cyclist which will be an an angle \theta with the vertical.
Let m be the mass of the cycle with the cyclist
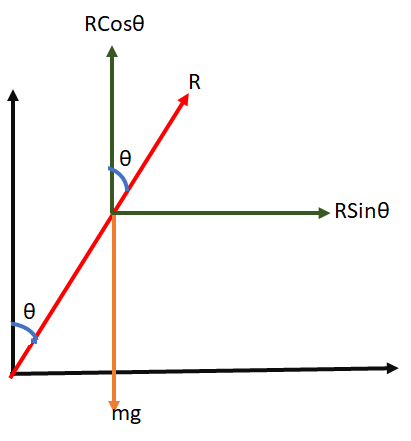
The vertical component RCos\theta balances the weight mg of the cyclist
The horizontal component RSin\theta gives the centripetal force to make the turn.
Then Rcos\theta = mg and
RSin\theta =\frac{mv^{2}}{r}
here v is the velocity of the cyclist
\frac{RSin\theta}{RCos\theta}=\frac{\frac{mv^{2}}{r}}{mg}
Numerical problems and solution on uniform circular motion
Numerical questions with answers on uniform circular motion, banking of roads and bending of a cyclist.
1. An object completes 8 revolutions in 2second, in a circular path of radius 1m. Find the angular velocity and linear speed.
Angular displacement for 1 revolution is 2\pi rad
So, Angular displacement for 8 revolution is 2\pi \times 8=16\pi rad
Angular displacement = 16\pi rad
Time = 2 s
Angular velocity, \omega = \frac{Angular displacement}{time}
Angular velocity, \omega = \frac{16\pi}{2} = 8\pi rad/s
radius r = 1m
linear velocity, v = \omega r = 8\pi \times 1 = 8\pi m/s
2. Calculate the centripetal force acting on a small mass of 0.25kg rotating 1800 rpm on a circular path of radius 200 mm.
mass of the object, m = 0.25 kg
radius, r = 200 mm = 0.2 m
Angular velocity, \omega = 1800 rpm
\omega=1800 \times \frac{2\pi}{60}=60\pi rad/s
Centripetal force, F=m\omega^{2}r
F=0.25 \times (60\pi)^{2} \times 0.2
F = 29.6 N
3. A stone of mass 2 kg is attached to a string of length 1 meter. The string can withstand maximum tension 200 N. What is the maximum speed that stone can have during the whirling motion?
mass of the stone, m = 2 kg
length of the string, l = 1 m
Tension, T = 200 N
Let v is the maximum speed that the stone can have so that the string remains intact.
Here the tension supplies the required centripetal force to the stone for the whirling motion. Then
\frac{mv^{2}}{l}=T
v^{2}=\frac{lT}{m}
v=\sqrt{\frac{lT}{m}}
v=\sqrt{\frac{1\times 200}{2}}
v=10 m/s
So, the maximum speed of the stone can be 10 m/s
4. A car takes a turn with velocity 50 ms-1 on the circular road of radius of curvature 10 m. calculate the centrifugal force experienced by a person of mass 60kg inside the car?
mass of the person, m = 60 kg
radius of curvature of the road, r = 10 m
velocity of the car, v = 50 m/s
Centrifugal force, F = \frac{mv^{2}}{r}
F = \frac{60 \times (50)^{2}}{10}
F=15000 N = 1.5 kN
5. An electric train has to travel a curved railway line of radius 50m with maximum speed of 36 kmph. Calculate the angle through which the outer rail should be raised so that there is no lateral thrust on the rails.
radius of the curved railway line, r = 50 m
Speed of the train, v = 36 km/h = \frac{36\times 1000}{3600} m/s = 10 m/s
Let the angle of banking be \theta
Then, tan\theta =\frac{v^{2}}{rg}
tan\theta =\frac{(10)^{2}}{50 \times 9.8}
tan\theta =0.204
\theta = 11.53^{0}
6. A scooter rider negotiates a curve of 100m radius on a level road with a speed of 72 kmph. Calculate the angle of inclination to the vertical he should make to avoid falling.
radius of the curved road, r = 100 m
Speed of the train, v = 72 km/h = \frac{72\times 1000}{3600} m/s = 20 m/s
Let the angle of inclination to the vertical be \theta
Then, tan\theta =\frac{v^{2}}{rg}
tan\theta =\frac{(20)^{2}}{100 \times 9.8}
tan\theta =0.408
\theta = 22.195^{0}<