Questions and answers on Wave motion and its applications. This chapter is important for Engineering physics course (both diploma and bachelor). This chapter contain questions and numerical from the following topics
Simple Harmonic Motion
Wave Motion
Acoustics of building (Reverberation )
Table of contents
MCQ questions on wave motion and its applications
Short answer type questions with answers
Numerical problems with answers on Wave motion and its applications
MCQ questions with answers on Wave motion and its applications
1. The unit of frequency is
(a) s, (b) newton, (c) Hz, (d) Henry
option c
2. The velocity of a particle executing simple harmonic motion is maximum at
(a) At the extreme position
(b) At the mean position
(c) At a point between mean and extreme position
(d) constant throughout its motion
option b
3. In SHM (simple harmonic motion ), the acceleration is proportional to
(a) displacement, (b) velocity, (c) force, (d) None of the above
option a
4. The total energy in SHM
(a) decreases with time
(b) increases with time
(c) remain constant
option c
5. The relation between time period (T) and frequency (f) is
(a) T = f, (b) T=1/f, (c) T = \sqrt{f}, (d) f = \sqrt{T}
option b
6. Sound wave is
(a) longitudinal wave, (b) Transverse wave
option a
Short answer type questions with answers on Wave motion and its applications
1. Define SHM. Give some examples
Simple harmonic motion is defined as a motion in which the force is directly proportional to the displacement of the body from a fixed point and is always directed towards the fixed point.
Force , F \propto -x , where x is the displacement
and acceleration, a \propto -x
Examples: 1. Motion of a simple pendulum
2. Vibrations of a spring mass system
2. What are the characteristics of a simple harmonic motion.
option c
i. The motion is periodic and oscillatory.
ii. Restoring force is directly proportional to the displacement of the body.
iii. Acceleration of the body is directly proportional to the displacement .
iv. Velocity is maximum at the extreme position and minimum at the mean position.
v. Total mechanical energy remain constant.
3. Show that the total mechanical energy of a harmonic oscillator is constant.
Total mechanical energy = kinetic energy + potential energy
The kinetic energy of a particle of mass m is
K.E = \frac{1}{2}mv^{2}
K.E = \frac{1}{2}m(\pm \omega \sqrt{A^{2}-x^{2}})^{2}
Where, velocity v = (\pm \omega \sqrt{A^{2}-x^{2}})
\omega is the angular frequency and A is the amplitude and x is the displacement
K.E = \frac{1}{2}m \omega^{2}( {A^{2}-x^{2}})
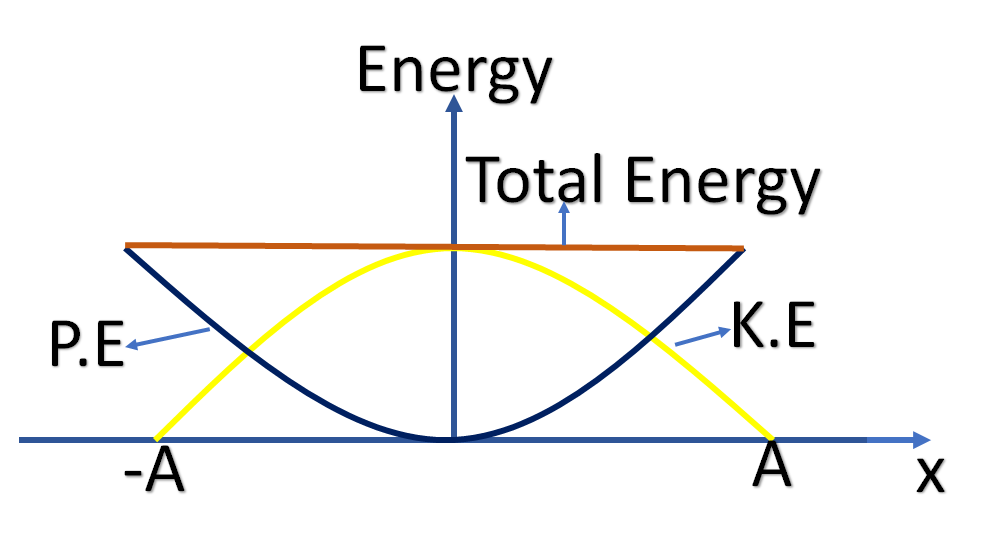
The force acting on the particle is F=-m\omega^{2}x
The work done to displace the particle by a distance dx against the restoring force is
dW=Fdx= m\omega^{2}xdx
So, the total work done in moving the particle from mean position to a distance x is
W=\int_{0}^{x} m\omega^{2}xdx
W=m\omega^{2}\int_{0}^{x} xdx
W=\frac{1}{2}m \omega^{2}x^{2}
This is stored as potential energy in the body. So, potential energy
P.E = \frac{1}{2}m \omega^{2}x^{2}
Total energy,
E = K.E + P.E
E = \frac{1}{2}m \omega^{2}( {A^{2}-x^{2}})+\frac{1}{2}m \omega^{2}x^{2}
E=\frac{1}{2}m \omega^{2}A^{2}
Total energy E is independent of x. So, it remains constant through out the motion of the particle.
4. What is free, damped and forced vibrations?
Free vibration: The vibration of a particle in the absence of any external force is called free vibration. The amplitude of vibration remain constant.
Damped vibration: In the presence of any external dissipating force, the amplitude of the oscillating body decreases with time is called damped vibration.
Forced Vibration: When a body oscillates under the influence of an external periodic force is called forced vibration.
5. What is a cantilever?
A cantilever is a rigid rod or beam supported at one end and loaded at the other.
6. What is reverberation time? Write down the expression of reverberation time of Sabine formula.
Sound in a room repeatedly comes from the walls, celling, windows etc. The time required for the sound to decay or fade away is called reverberation time.
The formula for reverberation time according to Sabine is
T=\frac{0.16V}{aS}
Where V is the volume of the room
a is the co-efficient of absorption
a=\frac{sound \hspace{0.2cm} energy \hspace{0.2cm}absorbed \hspace{0.2cm}by\hspace{0.2cm} the\hspace{0.2cm} surface}{total \hspace{0.2cm}energy\hspace{0.2cm} incident\hspace{0.2cm} on\hspace{0.2cm} the\hspace{0.2cm} surface}
S is the area of the reflecting surface
7. What is ultrasonic wave. Write some applications of ultrasound wave.
Ultrasonic waves are sound waves whose frequencies are higher than the audible frequencies to human ear. The frequency is greater than 20 kHz.
Application of Ultrasonic Waves: i. Ultrasonic waves are used to detect crack in a material.
ii. It is used in sound navigation and ranging (SONAR).
iii. Used in medical science (Ultrasonography, echocardiography)
Numerical problems with answers on Wave motion and its applications
1. If a simple pendulum oscillates with an amplitude of 50 mm and time period of 2 s, then its maximum velocity is
(a) 0.8 m/s, (b) 0.15 m/s, (c) 0.10 m/s, (d) 0.16 m/s
option d
We know the velocity of a simple pendulum is v=\pm \omega \sqrt{A^{2}-x^{2}}
Maximum velocity is at x = 0
So maximum velocity is v = \omega A = \frac{2\pi}{T}A
Here, time period T = 2 s and amplitude A = 50mm = 0.050 m
v=\frac{2\pi}{2}\times 0.050
v=0.157 = 0.16 m/s
2. If a spring of mass 30 kg has spring constant of 15 N/m, then its time period is
(a) 2\pi s, (b) 2\sqrt{2\pi} s, (c) 2\sqrt{2} s, (d) 2\pi\sqrt{2} s
option d
The time period of a spring mass system is
T=2\pi\sqrt{\frac{m}{k}}
mass of the spring, m = 30 kg
spring constant, k = 15 N/m
T=2\pi\sqrt{\frac{30}{15}}
T=2\pi\sqrt{2} s
3. A particle executes simple harmonic motion with an angular velocity and maximum acceleration of 3.5 rad/s and 7.5 m/s2 respectively. Amplitude of the oscillation is
(a) 0.36m, (b) 0.28m, (c) 0.61m, (d) 0.53m
option c
angular velocity, \omega = 3.5 rad/s
maximum acceleration, a = 7.5 m/s2
We know that acceleration a=- \omega^{2}x
So, acceleration is maximum when x =A (A is the amplitude)
So, a=\omega^{2}A
A=\frac{a}{\omega ^{2}}
A=\frac{7.5}{3.5 ^{2}}
A = 0.61 m
4. A simple pendulum performs simple harmonic motion about x=0 with an amplitude a and time period T. The speed of the pendulum at x=a/2 will be
(a) \frac{\pi a}{T} (b) \frac{3\pi ^{2} a }{T} (c) \frac{\pi a \sqrt{3}}{T}, (d) \frac{\pi a \sqrt{3}}{2T}
option c
velocity, v= \omega \sqrt{a^{2}-x^{2}}
\omega = \frac{2\pi}{T}
v= \frac{2\pi}{T} \sqrt{a^{2}-x^{2}}
x=a/2
v= \frac{2\pi}{T} \sqrt{a^{2}-(\frac{a}{2})^{2}}
v= \frac{2\pi}{T} \sqrt{a^{2}-\frac{a^{2}}{4}}
v= \frac{2\pi}{T} \sqrt{\frac{3a^{2}}{4}}
v= \frac{\pi a \sqrt{3}}{T}
5. If equation of sound wave is y=0.0015Sin(62.4x+316t), then its wavelength will be
(a) 0.2 unit, (b) 0.3 unit, (c) 0.1 unit, (d) 2 unit
option c
y=0.0015Sin(62.4x+316t)
Comparing the above equation with y=ASin(kx+ \omega t)
A=0.0015
k=62.4
\omega = 316
We know that,
k=\frac{2\pi}{\lambda}
\lambda=\frac{2\pi}{k}
\lambda=\frac{2\pi}{62.4} =0.1 unit